今回は皆さんお待ちかね、インテグラルイメージングで撮影した画像から3次元画像を得る最も簡単な方法を紹介します。
インテグラルイメージングについて簡単に復習しておくと、
- 多視点の写真が得られ、そこには無数の視差が存在する
- とりあえずすべての写真をずらして重ねれば、どこかに焦点が合う
インテグラルイメージングの論文では多視点写真のことを3次元要素が詰まった情報源という意味から要素画像(Elemental image)、そこから3次元映像を得ることを再構成(Reconstruction)と呼びます。 今日紹介するのはその最も基本的な体積的計算機再構成(Volumetric computational reconstruction)です。 日本語にすると変な感じなので自分はもっぱらVCRという略語を使います。
ここで少し引っかかるのは計算機(パソコン)を用いているということです。 言ってしまえばこれはシミュレーションで、本当の再構成とは光学的なものなので、まずそちらを簡単に紹介します。
光学的再構成(Optical reconstruction)
インテグラルイメージングは3次元空間をレンズアレイを用いて撮影する手法です。 そこから3次元の映像をもっとも簡単に戻す方法 … それは撮影した要素画像をプロジェクターや液晶で表示し、その前に撮影時と同じレンズアレイを置くことによる逆変換です。
こちらに素晴らしい動画があったので紹介します。 これは印刷物の上にレンズアレイを置くことで実現しています。
さて原理を簡単に図にまとめます。
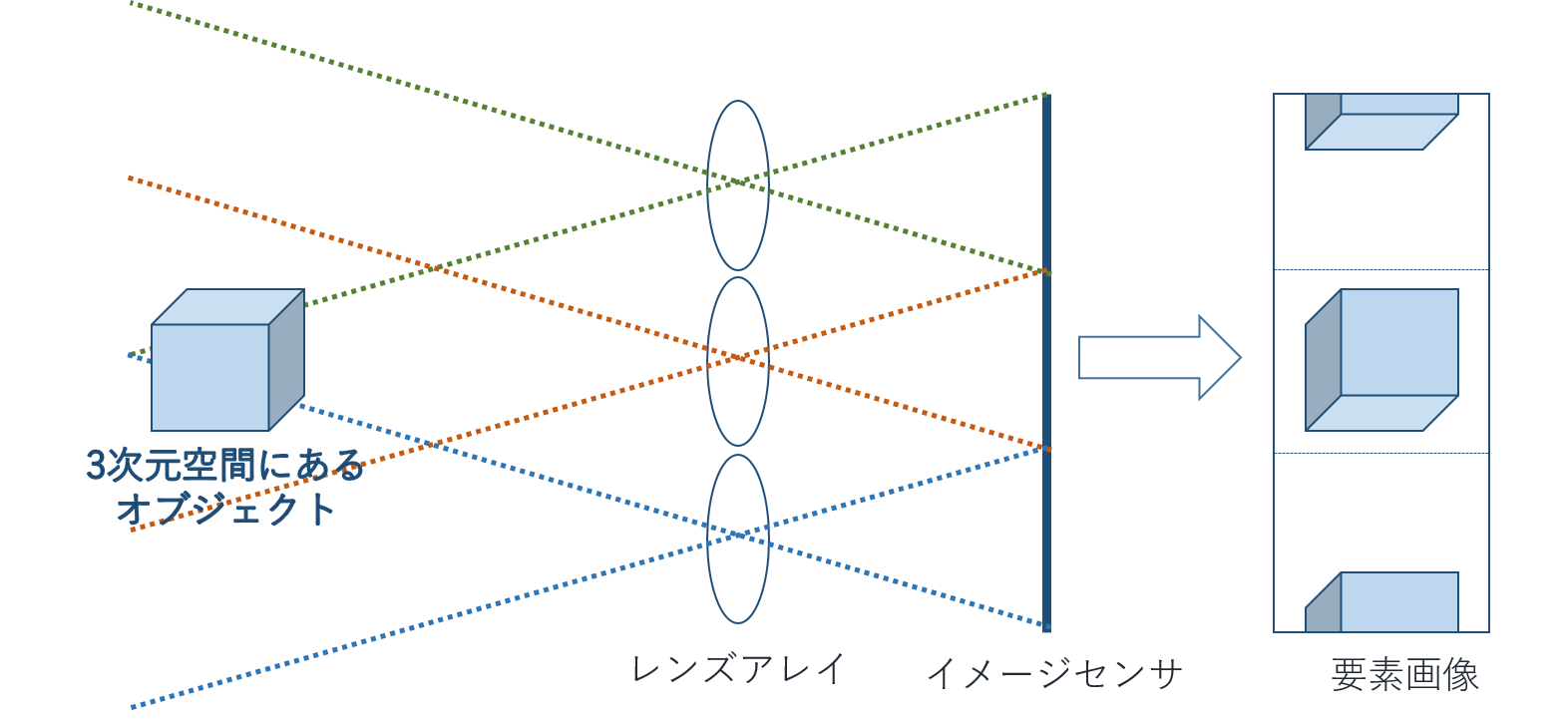
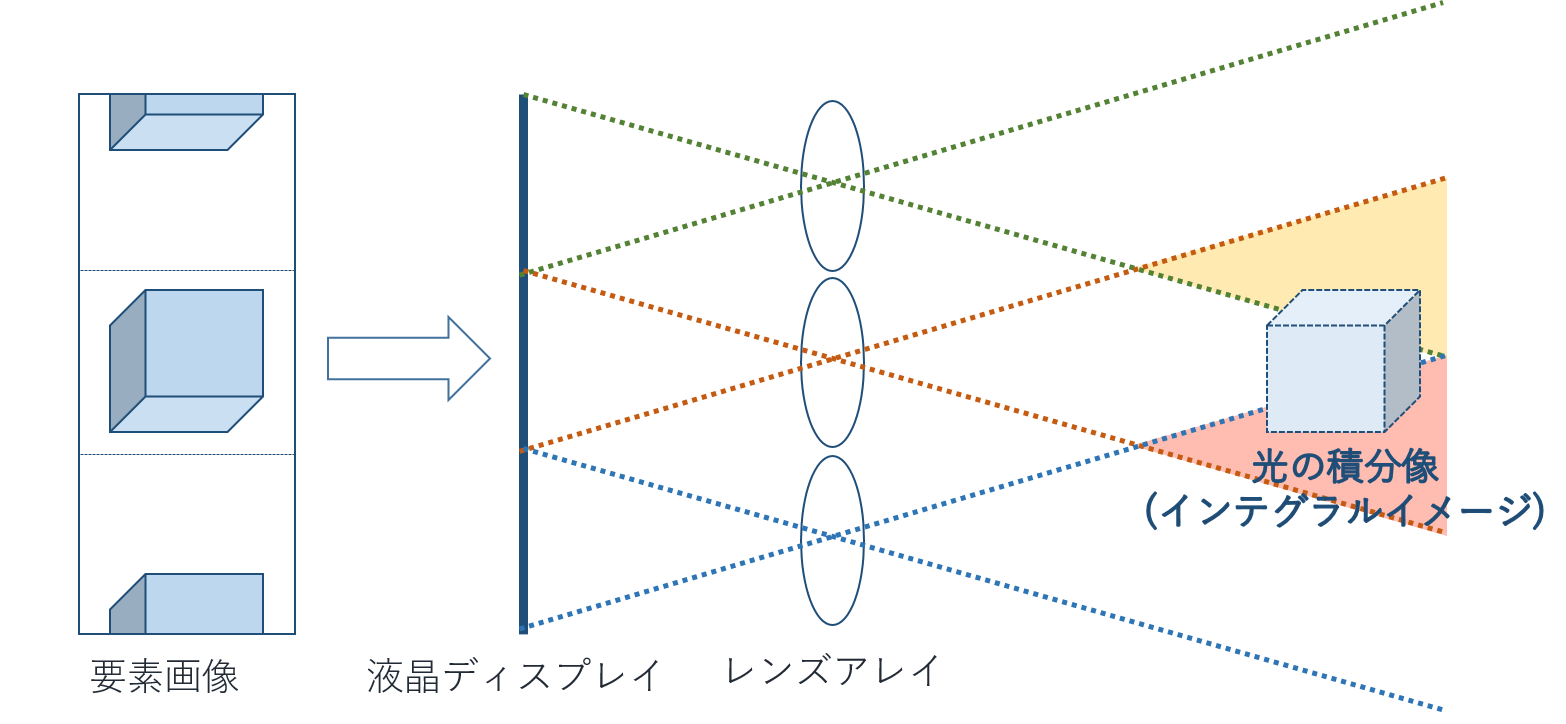
再構成の図から、インテグラルイメージングがなぜ「積分画像法」という名前がついているのか、懸命な読者諸君ならもうおわかりですね?(一度書いてみたかっただけ) 簡単にまとめると各視点の画像をレンズで拡大して重ね合わせる(積分)画像ということです。
ここでまたいかにも説明したそうな色が再構成の画像についていますね? 黄色とオレンジの三角領域は画像の重なりを示しています。 これが意味するところは、距離が離れるほど隣接する視点の画像との重畳領域が増えるということです。 つまり、わざわざ写真を拡大しなくとも、各視点の画像をずらして重ねると同じ効果が得られることを示しています。
これに気づいたえらい学者さんが計算機による光学的再構成をシミュレートしたもの、そのアルゴリズムがVCRです。
VCR (Volumetric computational reconstruction)
そもそもなぜ光学的に簡単にできてしまうことをパソコンでする必要があるのかをはじめに説明します。
それはなんといってもデジタルデータの扱いやすさです。
また前回の投稿でも説明したように、インテグラルイメージングはその原理から高解像度化が苦手です。
レンズに工夫を凝らすのも良いですが、ハードウェアの試作と改良は金がかかって仕方がないので(T_T)…(ちょっとうちはNGなんすよ…)
そこをなんとか超えるために、インテグラルイメージングの研究者はデジタル画像処理のアプローチで様々なアルゴリズムを検討しています。
さて前置きもほどほどに中身を説明しましょう。 今回は簡単化のために2視点のステレオ画像の場合の画像の重なりを考えてみます。 言葉の定義は以下の図に示します。
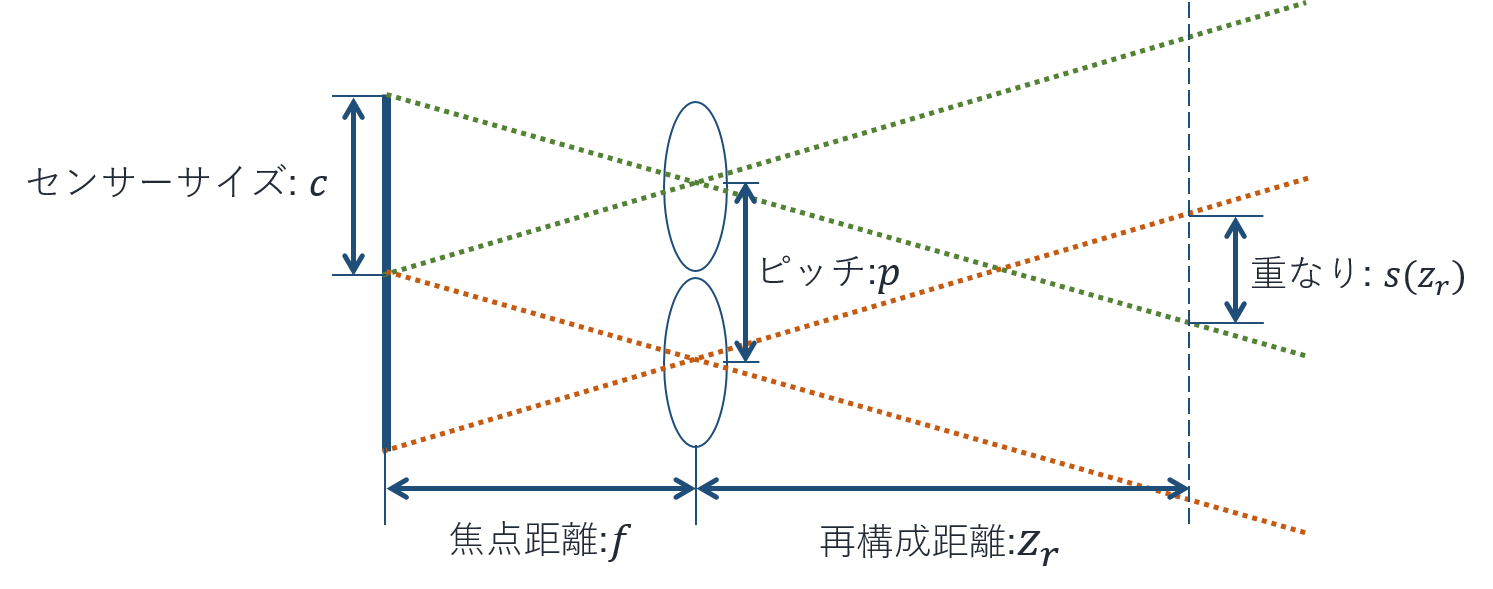
重なり量の導出
ここから途中式を一切省略せずに丁寧に導出しますが、面倒な人は次節まで飛ばして大丈夫です。
ちょっと重なり量の導出には遠いので、一つ目のレンズの中心を座標0とした場合、次のように書き換えられます。 矢印は便宜上ずらして描かれていますが、実際は同じ再構成距離で重なっているものとします。
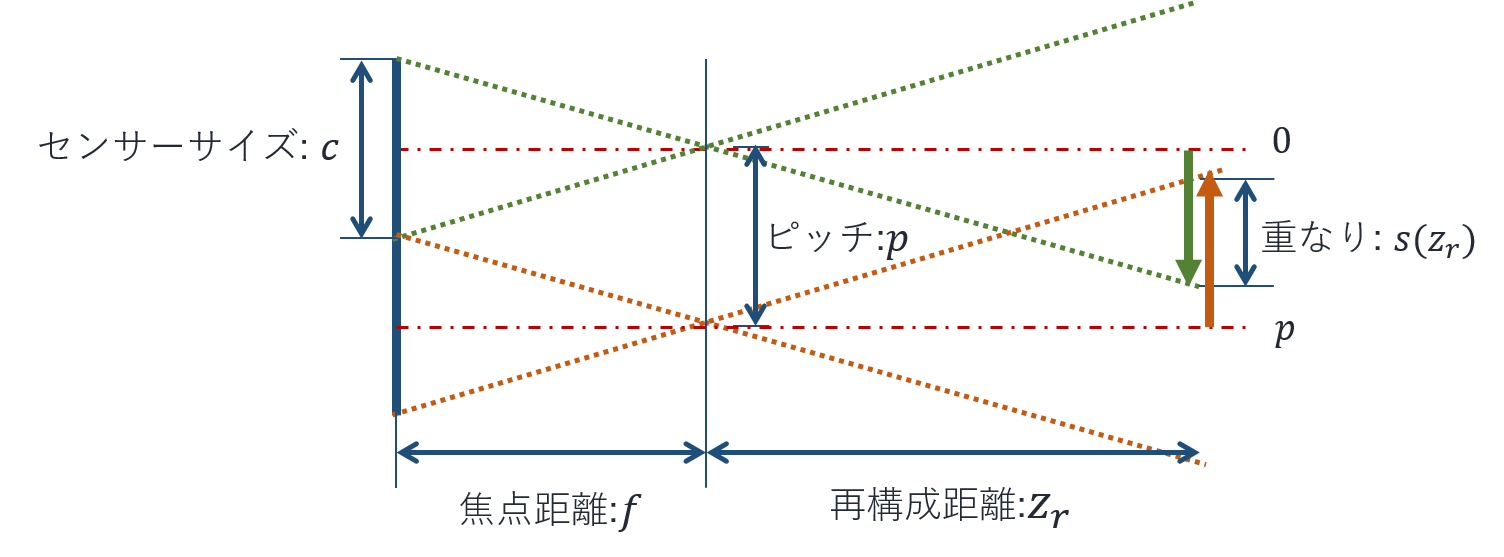
このとき重なり始めは上から数えて2つ目の画像の終端からであり、終わりは1つ目の画像の始端です。 再構成距離$z_r$において拡大されたセンサーサイズ$c$はレンズの拡大率$m(z_r)=z_r/f$をかけて$cm(z_r)$となります。つまり、ある再構成距離$z_r$における重なりを関数の形式で$s(z_r)$と表すと、矢印の長さは$cm(z_r)/2$から、
\begin{align} s(z_r) &= z_rにおける1つ目の画像の始端-z_rにおける2つ目の画像の始端\newline &= \frac{cm(z_r)}{2}-\left(p-\frac{cm(z_r)}{2}\right)\newline &= cm(z_r)-p. \end{align}
これは物理的な距離なので、1視点の画像一枚あたりの割合で示したほうが扱いやすいです。重なり率を$s_r(z_r)$とすると、
\begin{align} s_r(z_r) &= \frac{z_rにおける重なり}{z_rにおけるセンサーサイズ} =\frac{s(z_r)}{cm(z_r)}. \end{align}
最終的にはこの割合からデジタル写真において、何ピクセル重なっているかを知る必要があるので、1視点あたりの画像の解像度を$r$とすると、ピクセル換算の重なり量$s_p(z_r)$は
\begin{align} s_p(z_r) &= 1視点あたりの解像度 \times z_rにおける重なり率 \newline &=rs_r(z_r). \end{align}
以上がピクセル単位での重なり量の導出でした。 実際の計算には画像ごとにずらして重ねるためのずらし量が知りたいので、解像度から重なり量を引いたズレ量を用います。 念のため示しておくと、ズレ量$s_{h}(z_r)$は \begin{align} s_h(z_r) &= 1視点あたりの解像度 - z_rにおける重なり量\newline &= r-s_p(z_r)\newline &= r(1-s_r(z_r))\newline &= r\left(1-\frac{s(z_r)}{cm(z_r)}\right)\newline &= r\left(1-\frac{cm(z_r)-p}{cm(z_r)}\right)\newline &= r\left(1-1+\frac{p}{cm(z_r)}\right)\newline &= \frac{rp}{c\frac{f}{z_r}}\newline &= \frac{z_rrp}{fc}. \end{align}
と最終的には非常にシンプルな式が導出されます。満足。 書いてから気づきましたけど、これ重なり量からではなくズレ量を直接導出したほうが良かったです…?
画像の重ね合わせ
ある再構成距離$z_r$における、視点ごとの画像のズレ量$s_h(z_r)$は$\frac{z_rrp}{fc}$で計算できることがわかりました。 あとはこれらをすべてずらしながら重ね、最終的に重畳数で除算して輝度を整えていっちょあがりです。 コードはこちらからダウンロードできます。ちなみにPython3系でしか動かないと思います。
コードはVCR_lensarray.pyとVCR_saii.pyの2つありますが、これは要素画像の撮影方法の違いを意味します。 レンズアレイタイプはそのままレンズアレイを使って撮影した、伝統的(?)なスタイル。 SAII(Synthetic Aperture Integral Imaging)はレンズアレイの代わりにカメラアレイを用いた手法です。 2つの処理の違いは要素画像の各視点画像を上下左右に反転しているかだけです。
まとめ
- ずらして重ねるだけで3Dスライス画像が得られる
まとめの雑さには目をつむり、さらなるディープな高解像度化手法はのちのち。
次は要素画像のBlenderでのシミュレーション方法を書こうと思います。
参考文献
Three-dimensional volumetric object reconstruction using computational integral imaging. [Optics Express Vol.12, No.3, 483,(2004)]
Three-dimensional synthetic aperture integral imaging. [Optics Letter Vol.27, Issue 13,1144, (2002)]